CUERPOS GEOMÉTRICOS II

EL CONO

Juan Ramón

En geometría, un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro cateto se denomina Base y al punto donde confluyen las generatrices se llama vértice.

 Cilindro

Cristian Ortiz Contreras

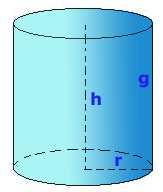
En geometría, un cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, que puede ser cerrada o abierta, denominada directriz del cilindro.
Si la directriz es un círculo y la generatriz es perpendicular a él, entonces la superficie obtenida, llamada cilindro circular recto, será de revolución y tendrá por lo tanto todos sus puntos situados a una distancia fija de una línea recta, el eje del cilindro. El sólido encerrado por esta superficie y por dos planos perpendiculares al eje también es llamado cilindro. Este sólido es utilizado como una superficie Gausiana.
En geometría diferencial, un cilindro se define de forma general como cualquier superficie reglada generada por una familia uniparamétrica de líneas paralelas.

La pirámide

                                                      Agustin
Una pirámide es un poliedro limitado por una base, que es un polígono con una cara; y por caras, que son triángulos coincidentes en un punto denominado ápice.
El ápice o cúspide también es llamado vértice de la pirámide, aunque una pirámide tiene más vértices, tantos como el número de polígonos que lo limitan.

EL CUBO

Moisés Gonzalez Barrul

Un cubo o hexaedro regular es un poliedro de seis caras cuadradas congruentes, siendo uno de los llamados sólidos platónicos.
Un cubo, además de ser un hexaedro, puede ser clasificado también como paralelepípedo, recto y rectángulo, pues todas sus caras son de cuatro lados y paralelas dos a dos, e incluso como un prisma de base cuadrangular y altura equivalente al lado de la , pues tiene seis caras, ocho vértices y doce aristas (8+6=12+2).

 Prisma

Luis

• En geometría, un prisma es un sólido determinado por dos polígonos paralelos y congruentes que se denominan bases y por tantos paralelogramos como lados tengan las bases, denominados caras.